897.Increasing Order Search Tree
Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
Example 1:
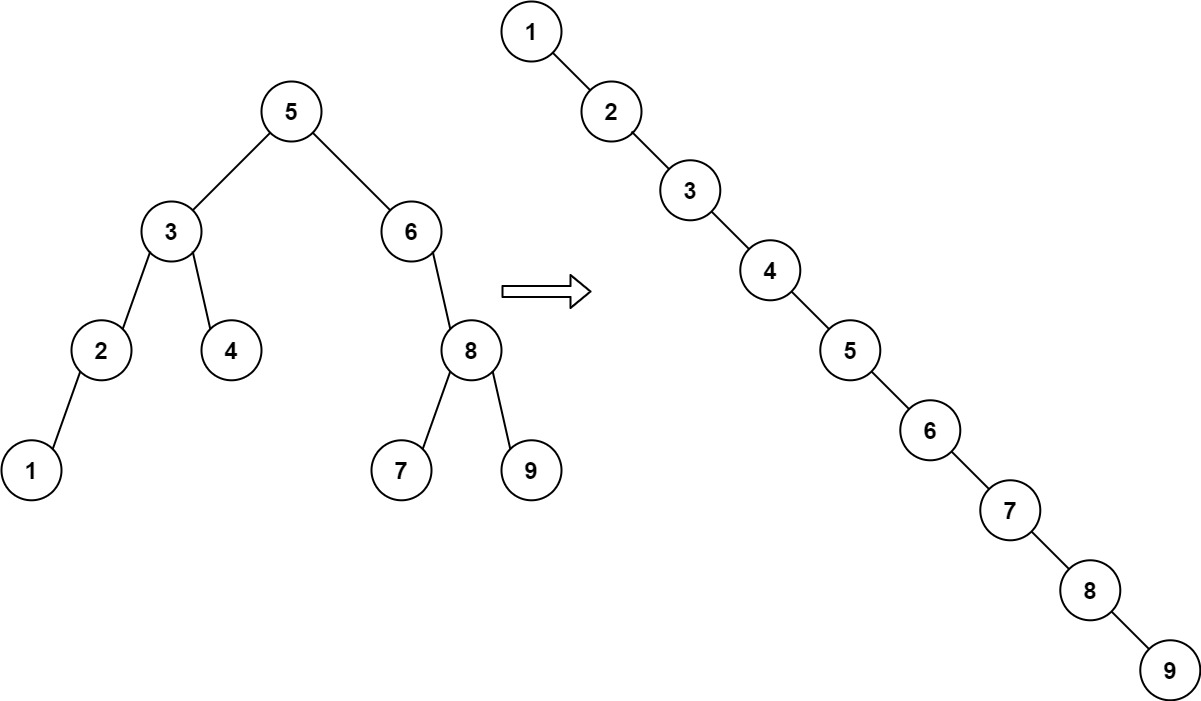
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
Example 2:
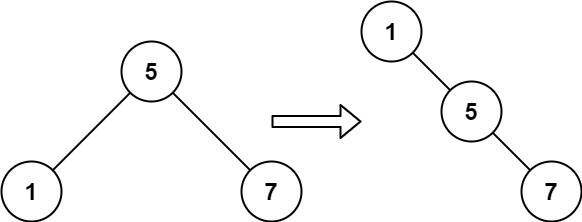
Input: root = [5,1,7]
Output: [1,null,5,null,7]
Constraints:
- The number of nodes in the given tree will be in the range
[1, 100]. 0 <= Node.val <= 1000
class Solution {
public TreeNode increasingBST(TreeNode root) {
List<Integer> vals = new ArrayList();
inorder(root, vals);
TreeNode ans = new TreeNode(0), cur = ans;
for (int v: vals) {
cur.right = new TreeNode(v);
cur = cur.right;
}
return ans.right;
}
public void inorder(TreeNode node, List<Integer> vals) {
if (node == null) return;
inorder(node.left, vals);
vals.add(node.val);
inorder(node.right, vals);
}
}
Approach 2: Traversal with Relinking
Intuition and Algorithm
We can perform the same in-order traversal as in Approach 1. During the traversal, we’ll construct the answer on the fly, reusing the nodes of the given tree by cutting their left child and adjoining them to the answer.
class Solution {
TreeNode cur;
public TreeNode increasingBST(TreeNode root) {
TreeNode ans = new TreeNode(0);
cur = ans;
inorder(root);
return ans.right;
}
public void inorder(TreeNode node) {
if (node == null) return;
inorder(node.left);
node.left = null;
cur.right = node;
cur = node;
inorder(node.right);
}
}
938,Range Sum of BST
Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].
Example 1:
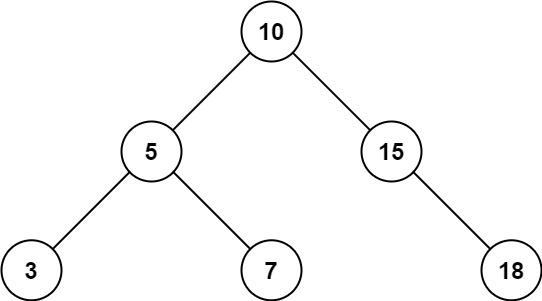
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32
Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.
Example 2:
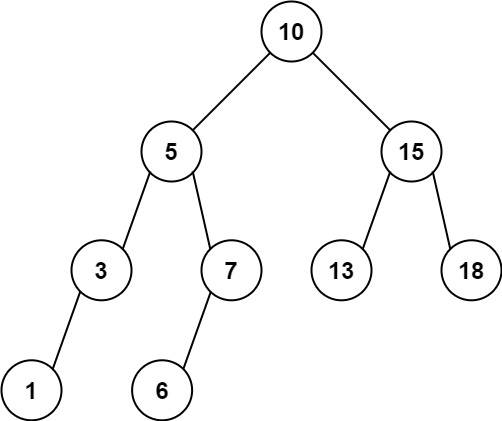
Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
Output: 23
Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.
Constraints:
- The number of nodes in the tree is in the range
[1, 2 * 104]. 1 <= Node.val <= 1051 <= low <= high <= 105- All
Node.valare unique.
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int sum = 0;
public void addValueToSum(TreeNode root,int low,int high){
if (root == null) return;
if (root.val<low){
//ignore left
addValueToSum(root.right,low,high);
}else if(root.val == low) {
sum += root.val;
addValueToSum(root.right,low,high);
}else if(root.val>high) {
//ignore right
addValueToSum(root.left,low,high);
}else{
//left and right
sum += root.val;
addValueToSum(root.left,low,high);
addValueToSum(root.right,low,high);
}
}
public int rangeSumBST(TreeNode root, int low, int high) {
addValueToSum(root,low,high);
return sum;
}
}
Iterative Implementation
class Solution {
public int rangeSumBST(TreeNode root, int low, int high) {
int ans = 0;
Stack<TreeNode> stack = new Stack();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
if (node != null) {
if (low <= node.val && node.val <= high)
ans += node.val;
if (low < node.val)
stack.push(node.left);
if (node.val < high)
stack.push(node.right);
}
}
return ans;
}
}
965.Univalued Binary Tree
A binary tree is uni-valued if every node in the tree has the same value.
Given the root of a binary tree, return true if the given tree is uni-valued, or false otherwise.
Example 1:
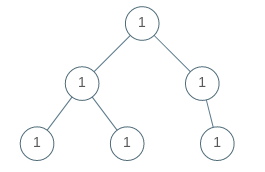
Input: root = [1,1,1,1,1,null,1]
Output: true
Example 2:
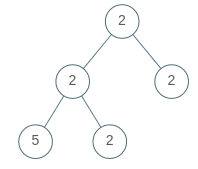
Input: root = [2,2,2,5,2]
Output: false
Constraints:
- The number of nodes in the tree is in the range
[1, 100]. 0 <= Node.val < 100
if this tree is BST
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int firstValue = 0;
public boolean isMinEqual(TreeNode root){
if(root == null) return true;
if(root.val != firstValue) return false;
return isMinEqual(root.left);
}
public boolean isRightEqual(TreeNode root){
if(root == null) return true;
if(root.val != firstValue) return false;
return isRightEqual(root.right);
}
public boolean isUnivalTree(TreeNode root) {
firstValue = root.val;
return isMinEqual(root) && isRightEqual(root);
}
}
if not
class Solution {
public boolean isUnivalTree(TreeNode root) {
boolean left_correct = (root.left == null ||
(root.val == root.left.val && isUnivalTree(root.left)));
boolean right_correct = (root.right == null ||
(root.val == root.right.val && isUnivalTree(root.right)));
return left_correct && right_correct;
}
}
public boolean isUnivalTree(TreeNode root) {
if(root == null)
return true;
if(root.left != null)
if(root.val != root.left.val)
return false;
if(root.right != null)
if(root.val != root.right.val)
return false;
return isUnivalTree(root.left) && isUnivalTree(root.right);
}
993.Cousins in Binary Tree
Given the root of a binary tree with unique values and the values of two different nodes of the tree x and y, return true if the nodes corresponding to the values x and y in the tree are cousins, or false otherwise.
Two nodes of a binary tree are cousins if they have the same depth with different parents.
Note that in a binary tree, the root node is at the depth 0, and children of each depth k node are at the depth k + 1.
Example 1:

Input: root = [1,2,3,4], x = 4, y = 3
Output: false
Example 2:

Input: root = [1,2,3,null,4,null,5], x = 5, y = 4
Output: true
Example 3:

Input: root = [1,2,3,null,4], x = 2, y = 3
Output: false
Constraints:
- The number of nodes in the tree is in the range
[2, 100]. 1 <= Node.val <= 100- Each node has a unique value.
x != yxandyare exist in the tree.
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
// To save the depth of the first node.
int recordedDepth = -1;
boolean isCousin = false;
private boolean dfs(TreeNode node, int depth, int x, int y) {
if (node == null) {
return false;
}
// Don't go beyond the depth restricted by the first node found.
if (this.recordedDepth != -1 && depth > this.recordedDepth) {
return false;
}
if (node.val == x || node.val == y) {
if (this.recordedDepth == -1) {
// Save depth for the first node found.
this.recordedDepth = depth;
}
// Return true, if the second node is found at the same depth.
return this.recordedDepth == depth;
}
boolean left = dfs(node.left, depth + 1, x, y);
boolean right = dfs(node.right, depth + 1, x, y);
// this.recordedDepth != depth + 1 would ensure node x and y are not
// immediate child nodes, otherwise they would become siblings.
if (left && right && this.recordedDepth != depth + 1) {
this.isCousin = true;
}
return left || right;
}
public boolean isCousins(TreeNode root, int x, int y) {
// Recurse the tree to find x and y
dfs(root, 0, x, y);
return this.isCousin;
}
}
1022,Sum of Root To Leaf Binary Numbers
You are given the root of a binary tree where each node has a value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit.
- For example, if the path is
0 -> 1 -> 1 -> 0 -> 1, then this could represent01101in binary, which is13.
For all leaves in the tree, consider the numbers represented by the path from the root to that leaf. Return the sum of these numbers.
The test cases are generated so that the answer fits in a 32-bits integer.
Example 1:
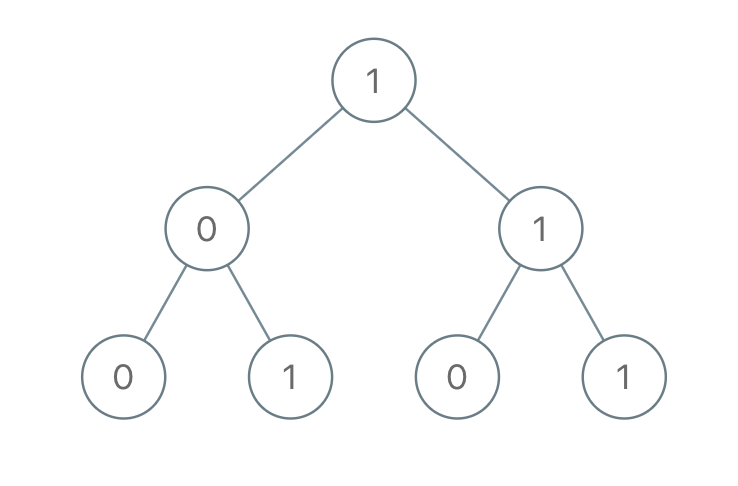
Input: root = [1,0,1,0,1,0,1]
Output: 22
Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
Example 2:
Input: root = [0]
Output: 0
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. Node.valis0or1.

class Solution {
int rootToLeaf = 0;
public void preorder(TreeNode r, int currNumber) {
if (r != null) {
currNumber = (currNumber << 1) | r.val;
// if it's a leaf, update root-to-leaf sum
if (r.left == null && r.right == null) {
rootToLeaf += currNumber;
}
preorder(r.left, currNumber);
preorder(r.right, currNumber);
}
}
public int sumRootToLeaf(TreeNode root) {
preorder(root, 0);
return rootToLeaf;
}
}
1379,Find a Corresponding Node of a Binary Tree in a Clone of That Tree
Given two binary trees original and cloned and given a reference to a node target in the original tree.
The cloned tree is a copy of the original tree.
Return a reference to the same node in the cloned tree.
Note that you are not allowed to change any of the two trees or the target node and the answer must be a reference to a node in the cloned tree.
Example 1:
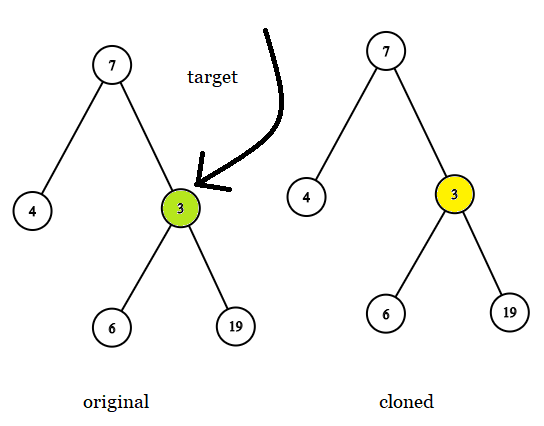
Input: tree = [7,4,3,null,null,6,19], target = 3
Output: 3
Explanation: In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.
Example 2:
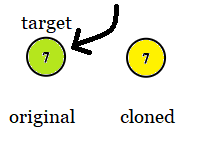
Input: tree = [7], target = 7
Output: 7
Example 3:
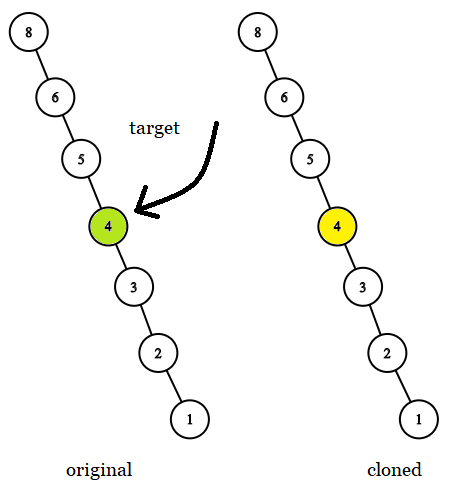
Input: tree = [8,null,6,null,5,null,4,null,3,null,2,null,1], target = 4
Output: 4
Constraints:
- The number of nodes in the
treeis in the range[1, 104]. - The values of the nodes of the
treeare unique. targetnode is a node from theoriginaltree and is notnull.
How to Solve
Let’s traverse both trees in parallel, and once the target node is identified in the first tree, return the corresponding node from the second tree.
How to Traverse the Tree: DFS vs BFS
There are two ways to traverse the tree: DFS depth first search and BFS breadth first search. Here is a small summary

Both are starting from the root and going down, both are using additional structures, what’s the difference? Here is how it looks at the big scale: BFS traverses level by level, and DFS first goes to the leaves.

Description doesn’t give us any clue which traversal is better to use here. Interview-simple solutions are DFS inorder traversals.
class Solution {
TreeNode ans, target;
public void inorder(TreeNode o, TreeNode c) {
if (o != null) {
inorder(o.left, c.left);
if (o == target) {
ans = c;
}
inorder(o.right, c.right);
}
}
public final TreeNode getTargetCopy(final TreeNode original, final TreeNode cloned, final TreeNode target) {
this.target = target;
inorder(original, cloned);
return ans;
}
}
1469, Find All The Lonely Nodes
In a binary tree, a lonely node is a node that is the only child of its parent node. The root of the tree is not lonely because it does not have a parent node.
Given the root of a binary tree, return an array containing the values of all lonely nodes in the tree. Return the list in any order.
Example 1:
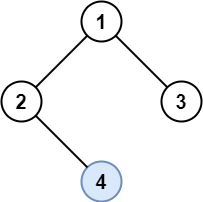
Input: root = [1,2,3,null,4]
Output: [4]
Explanation: Light blue node is the only lonely node.
Node 1 is the root and is not lonely.
Nodes 2 and 3 have the same parent and are not lonely.
Example 2:
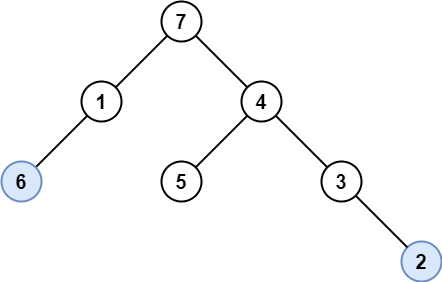
Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2]
Output: [6,2]
Explanation: Light blue nodes are lonely nodes.
Please remember that order doesn't matter, [2,6] is also an acceptable answer.
Example 3:
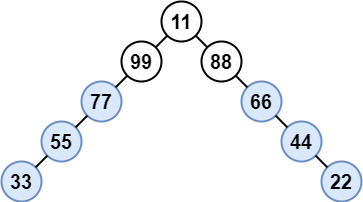
Input: root = [11,99,88,77,null,null,66,55,null,null,44,33,null,null,22]
Output: [77,55,33,66,44,22]
Explanation: Nodes 99 and 88 share the same parent. Node 11 is the root.
All other nodes are lonely.
Constraints:
- The number of nodes in the
treeis in the range[1, 1000]. 1 <= Node.val <= 106
class Solution {
public List<Integer> getLonelyNodes(TreeNode root) {
var nodes = new ArrayList<Integer>();
addLonelyNodes(nodes, root, false);
return nodes;
}
private static void addLonelyNodes(List<Integer> nodes, TreeNode root, boolean lonely) {
if (root == null) return;
if (lonely) nodes.add(root.val);
addLonelyNodes(nodes, root.left, root.right == null);
addLonelyNodes(nodes, root.right, root.left == null);
}
}

