637,Average of Levels in Binary Tree

Given the root of a binary tree, return the average value of the nodes on each level in the form of an array. Answers within 10-5 of the actual answer will be accepted.

Example 1:

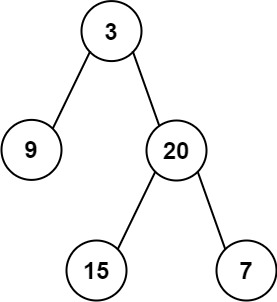
Input: root = [3,9,20,null,null,15,7]
Output: [3.00000,14.50000,11.00000]
Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.
Hence return [3, 14.5, 11].

Example 2:

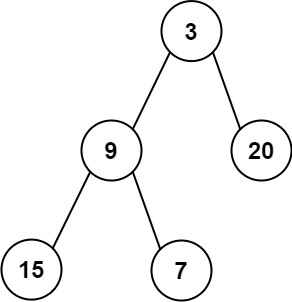
Input: root = [3,9,20,15,7]
Output: [3.00000,14.50000,11.00000]

Constraints:

The number of nodes in the tree is in the range [1, 104].
-231 <= Node.val <= 231 - 1

class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        
        List<Double> output = new ArrayList();
        Queue<TreeNode> queue = new LinkedList(); // First In First Out
        queue.add(root);
                
        Double rowSum = 0.0;
        int rowLen = 0;
        
        while(!queue.isEmpty()){
            rowSum = 0.0;
            rowLen = queue.size();
            
            for(int i = 0; i < rowLen; i++){ 
                TreeNode curr = queue.poll();
                rowSum += curr.val;
                if(curr.left != null){ queue.add(curr.left); }
                if(curr.right != null){ queue.add(curr.right); }
            }
            output.add(rowSum / rowLen);
        }
        return output;
    }
}

653,Two Sum IV - Input is a BST

Given the root of a binary search tree and an integer k, return true if there exist two elements in the BST such that their sum is equal to k, or false otherwise.

Example 1:

Input: root = [5,3,6,2,4,null,7], k = 9
Output: true

Example 2:

Input: root = [5,3,6,2,4,null,7], k = 28
Output: false

Constraints:

The number of nodes in the tree is in the range [1, 104].
-104 <= Node.val <= 104
root is guaranteed to be a valid binary search tree.
-105 <= k <= 105

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> l=new ArrayList<>();
    public boolean findTarget(TreeNode root, int k) {
        return help(root,k);
    }
    public boolean help(TreeNode root,int k )
    {
        if(root==null)return false;
        if(l.contains(k-root.val))return true;
        l.add(root.val);
        return help(root.left,k)||help(root.right,k);
    }
}

671.Second Minimum Node In a Binary Tree

Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly two or zero sub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes. More formally, the property root.val = min(root.left.val, root.right.val) always holds.

Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.

If no such second minimum value exists, output -1 instead.

Example 1:

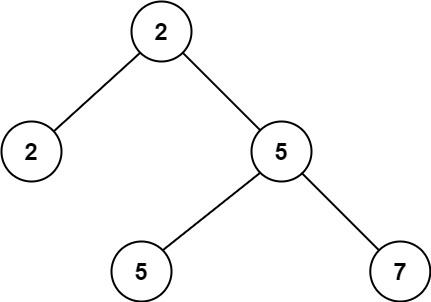
Input: root = [2,2,5,null,null,5,7]
Output: 5
Explanation: The smallest value is 2, the second smallest value is 5.

Example 2:

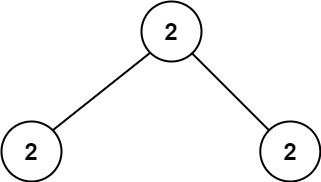
Input: root = [2,2,2]
Output: -1
Explanation: The smallest value is 2, but there isn't any second smallest value.

Constraints:

The number of nodes in the tree is in the range [1, 25].
1 <= Node.val <= 231 - 1
root.val == min(root.left.val, root.right.val) for each internal node of the tree.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int min=-1;
    int secondMin=Integer.MAX_VALUE;
    boolean flag=false;
    public int findSecondMinimumValue(TreeNode root) {
        if(root == null)return secondMin;
        min =root.val;
        help(root);
        if(!flag){return -1;}
        return secondMin;
    }
    public void help(TreeNode root){
        if(root == null)return;
        if(min< root.val && root.val<= secondMin){
            secondMin = root.val;
            flag = true;
        }
        help(root.left);
        help(root.right);
    }
}

700,Search in a Binary Search Tree

You are given the root of a binary search tree (BST) and an integer val.

Find the node in the BST that the node’s value equals val and return the subtree rooted with that node. If such a node does not exist, return null.

Example 1:

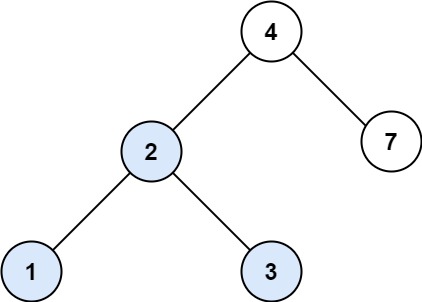
Input: root = [4,2,7,1,3], val = 2
Output: [2,1,3]

Example 2:

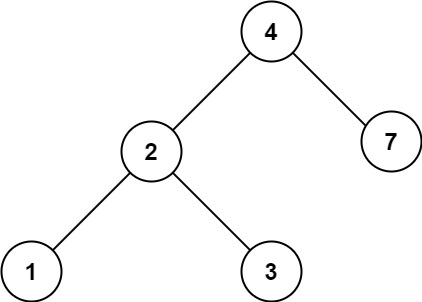
Input: root = [4,2,7,1,3], val = 5
Output: []

Constraints:

The number of nodes in the tree is in the range [1, 5000].
1 <= Node.val <= 107
root is a binary search tree.
1 <= val <= 107

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
     // space is O(n)
     public TreeNode searchBST(TreeNode root, int val) {
        if(root == null || root.val == val) return root;
        return root.val<val ? searchBST(root.right,val) :searchBST(root.left,val);
     }
}

class Solution {
 //space is O(1)
  public TreeNode searchBST(TreeNode root, int val) {
    while (root != null && val != root.val)
      root = val < root.val ? root.left : root.right;
    return root;
  }
}

703,Kth Largest Element in a Stream

Design a class to find the kth largest element in a stream. Note that it is the kth largest element in the sorted order, not the kth distinct element.

Implement KthLargest class:

KthLargest(int k, int[] nums) Initializes the object with the integer k and the stream of integers nums.
int add(int val) Appends the integer val to the stream and returns the element representing the kth largest element in the stream.

Example 1:

Input
["KthLargest", "add", "add", "add", "add", "add"]
[[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]
Output
[null, 4, 5, 5, 8, 8]

Explanation
KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]);
kthLargest.add(3);   // return 4
kthLargest.add(5);   // return 5
kthLargest.add(10);  // return 5
kthLargest.add(9);   // return 8
kthLargest.add(4);   // return 8

Constraints:

1 <= k <= 104
0 <= nums.length <= 104
-104 <= nums[i] <= 104
-104 <= val <= 104
At most 104 calls will be made to add.
It is guaranteed that there will be at least k elements in the array when you search for the kth element.

class KthLargest {
    private static int k;
    private PriorityQueue<Integer> heap;
    
    public KthLargest(int k, int[] nums) {
        this.k = k;
        heap = new PriorityQueue<>();
        
        for (int num: nums) {
            heap.offer(num);
        }
        
        while (heap.size() > k) {
            heap.poll();
        }
    }
    
    public int add(int val) {
        heap.offer(val);
        if (heap.size() > k) {
            heap.poll();
        }

        return heap.peek();
    }
}

783，Minimum Distance Between BST Nodes

Given the root of a Binary Search Tree (BST), return the minimum difference between the values of any two different nodes in the tree.

Example 1:

Input: root = [4,2,6,1,3]
Output: 1

Example 2:

Input: root = [1,0,48,null,null,12,49]
Output: 1

Constraints:

The number of nodes in the tree is in the range [2, 100].
0 <= Node.val <= 105

class Solution {
    // List to store the tree nodes in the inorder traversal.
    List<Integer> inorderNodes = new ArrayList<>();
    
    void inorderTraversal(TreeNode root) {
        if (root == null) {
            return;
        }
        
        inorderTraversal(root.left);
        // Store the nodes in the list.
        inorderNodes.add(root.val);
        inorderTraversal(root.right);
    }
    
    public int minDiffInBST(TreeNode root) {
       inorderTraversal(root);
        
        int minDistance = Integer.MAX_VALUE;
        // Find the diff between every two consecutive values in the list.
        for (int i = 1; i < inorderNodes.size(); i++) {
            minDistance = Math.min(minDistance, inorderNodes.get(i) - inorderNodes.get(i-1));
        }
        
        return minDistance;
    }
};

class Solution {
  int minDistance = Integer.MAX_VALUE;
  // Initially, it will be null.
  TreeNode prevValue;

  void inorderTraversal(TreeNode root) {
    if (root == null) {
      return;
    }

    inorderTraversal(root.left);

    // Find the difference with the previous value if it is there.
    if (prevValue != null) {
      minDistance = Math.min(minDistance, root.val - prevValue.val);
    }
    prevValue = root;

    inorderTraversal(root.right);
  }

  public int minDiffInBST(TreeNode root) {
    inorderTraversal(root);

    return minDistance;
  }
};

872,Leaf-Similar Trees

Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a leaf value sequence.

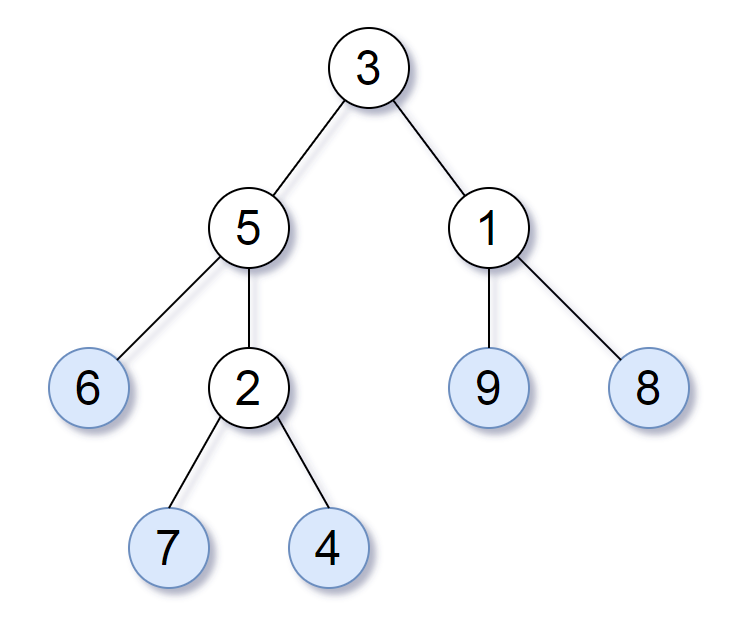
For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).

Two binary trees are considered leaf-similar if their leaf value sequence is the same.

Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.

Example 1:

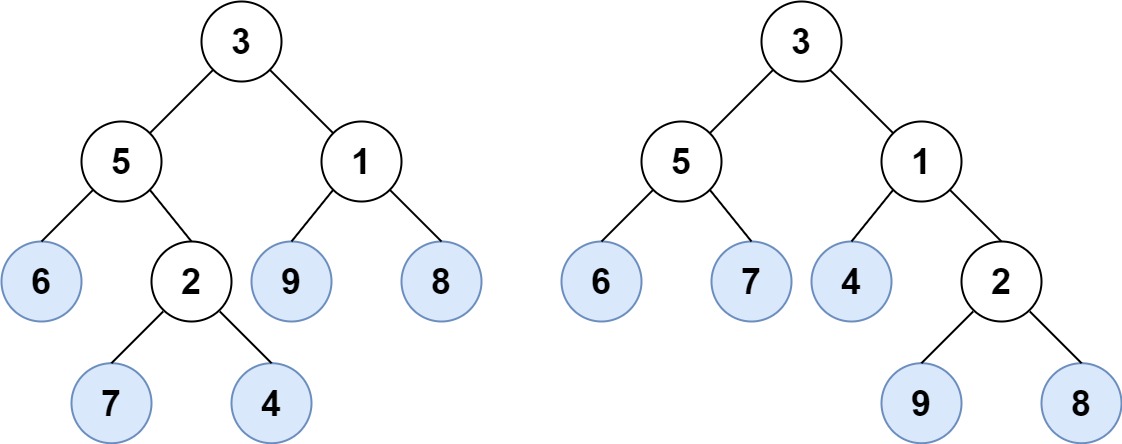
Input: root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8]
Output: true

Example 2:

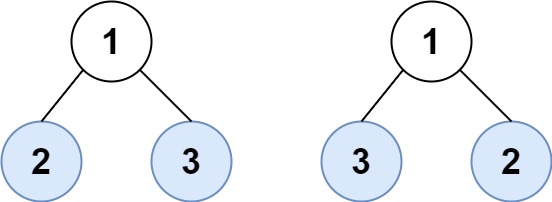
Input: root1 = [1,2,3], root2 = [1,3,2]
Output: false

Constraints:

The number of nodes in each tree will be in the range [1, 200].
Both of the given trees will have values in the range [0, 200].

Intuition and Algorithm

Let’s find the leaf value sequence for both given trees. Afterwards, we can compare them to see if they are equal or not.

To find the leaf value sequence of a tree, we use a depth first search. Our dfs function writes the node’s value if it is a leaf, and then recursively explores each child. This is guaranteed to visit each leaf in left-to-right order, as left-children are fully explored before right-children.

class Solution {
    public boolean leafSimilar(TreeNode root1, TreeNode root2) {
        List<Integer> leaves1 = new ArrayList();
        List<Integer> leaves2 = new ArrayList();
        dfs(root1, leaves1);
        dfs(root2, leaves2);
        return leaves1.equals(leaves2);
    }

    public void dfs(TreeNode node, List<Integer> leafValues) {
        if (node != null) {
            if (node.left == null && node.right == null)
                leafValues.add(node.val);
            dfs(node.left, leafValues);
            dfs(node.right, leafValues);
        }
    }
}

algorithm

637,Average of Levels in Binary Tree

653,Two Sum IV - Input is a BST

671.Second Minimum Node In a Binary Tree

700,Search in a Binary Search Tree

703,Kth Largest Element in a Stream

783，Minimum Distance Between BST Nodes

872,Leaf-Similar Trees

algorithm

algorithm