69,Sqrt(x)

Given a non-negative integer x, return the square root of x rounded down to the nearest integer. The returned integer should be non-negative as well.

You must not use any built-in exponent function or operator.

For example, do not use pow(x, 0.5) in c++ or x ** 0.5 in python.

Example 1:

Input: x = 4
Output: 2
Explanation: The square root of 4 is 2, so we return 2.

Example 2:

Input: x = 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.

Constraints:

0 <= x <= 231 - 1

Solution

class Solution {
    public int mySqrt(int x) {
        if(x==0) return 0;
        int low = 1,high = x,ans =0;
        while(low<=high){
            int mid =low + (high-low)/2;
            if(x/mid==mid)  return mid;
            else if(x/mid<mid)   high=mid-1;
            else {low = mid+1; ans = mid;}
        }
        return ans;
    }
}

94， Binary Tree Inorder Traversal

Given the root of a binary tree, return the inorder traversal of its nodes’ values.

Example 1:

Input: root = [1,null,2,3]
Output: [1,3,2]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [1]
Output: [1]

Constraints:

The number of nodes in the tree is in the range [0, 100].
-100 <= Node.val <= 100

Follow up: Recursive solution is trivial, could you do it iteratively?

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        helper(root, res);
        return res;
    }

    public void helper(TreeNode root, List<Integer> res) {
        if (root != null) {
            helper(root.left, res);
            res.add(root.val);
            helper(root.right, res);
        }
    }
}

100,Same Tree

Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

Example 1:

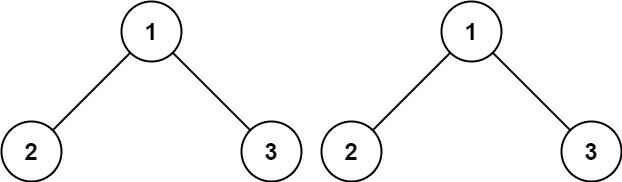
Input: p = [1,2,3], q = [1,2,3]
Output: true

Example 2:

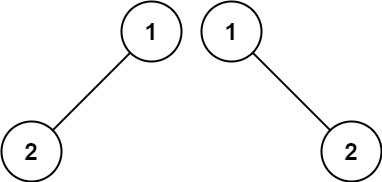
Input: p = [1,2], q = [1,null,2]
Output: false

Example 3:

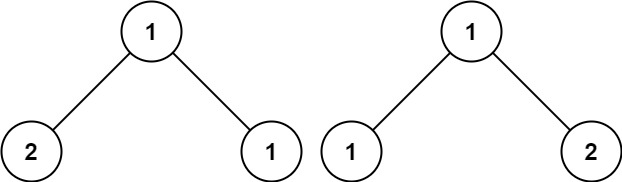
Input: p = [1,2,1], q = [1,1,2]
Output: false

Constraints:

The number of nodes in both trees is in the range [0, 100].
-104 <= Node.val <= 104

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
  public boolean isSameTree(TreeNode p, TreeNode q) {
    // p and q are both null
    if (p == null && q == null) return true;
    // one of p and q is null
    if (q == null || p == null) return false;
    if (p.val != q.val) return false;
    return isSameTree(p.right, q.right) &&
            isSameTree(p.left, q.left);
  }
}

101,Symmetric Tree

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

Example 1:

Input: root = [1,2,2,3,4,4,3]
Output: true

Example 2:

Input: root = [1,2,2,null,3,null,3]
Output: false

Constraints:

The number of nodes in the tree is in the range [1, 1000].
`-100 <= Node.val <= 100

Intuition

By seeing the problem my first intuition was to use BFS to solve the problem,by taking a queue but as i approached the problem i understand that using DFS is more optimal and less complex to solve this problem.

Approach

There are two parts of the tree - the left one and the right one. Some Observations :

The leftnode of left subtree is equal to the rightnode of right subtree.
Similarly the rightnode of left subtree is equal to the leftnode of right subtree.

So we can apply these recursively to check if the nodes are equal or not. If the tree is symmetric then the algorithm reaches the leaf nodes where each node is null, then we return true.

Complexity

Time complexity: O(n)
Space complexity: O(1)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }
        return checkSymmetric(root.left,root.right);
    }
    public boolean checkSymmetric(TreeNode leftNode,TreeNode rightNode){
        if(leftNode == null && rightNode == null){
            return true;
        }
        if(leftNode == null ^ rightNode == null){
            return false;
        }
        if(leftNode.val != rightNode.val){
            return false;
        }
        return checkSymmetric(leftNode.left,rightNode.right) && checkSymmetric(leftNode.right,rightNode.left);

    }
}

104,Maximum Depth of Binary Tree

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Constraints:

The number of nodes in the tree is in the range [0, 104].
-100 <= Node.val <= 100

class Solution {
    public int maxDepth(TreeNode root) {
        // Base Condition
        if(root == null) return 0;
        // Hypothesis
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        // Induction
        return Math.max(left, right) + 1;
    }
}

108,Convert Sorted Array to Binary Search Tree

Given an integer array nums where the elements are sorted in ascending order, convert it to a

*height-balanced*

binary search tree.

Example 1:

Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted:

Example 2:

Input: nums = [1,3]
Output: [3,1]
Explanation: [1,null,3] and [3,1] are both height-balanced BSTs.

Constraints:

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums is sorted in a strictly increasing order.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return CreateBST(nums, 0, nums.length - 1);
    }

    private TreeNode CreateBST(int nums[], int left, int right) {
        if (left > right) return null;
        int m = (right + left) / 2;
        TreeNode root = new TreeNode(nums[m]);
        root.left = CreateBST(nums, left, m - 1);
        root.right = CreateBST(nums, m+ 1, right);
        return root;
    }
}

110,Balanced Binary Tree

Given a binary tree, determine if it is

height-balanced

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

Constraints:

The number of nodes in the tree is in the range [0, 5000].
-104 <= Node.val <= 104

class Solution {
    public boolean isBalanced(TreeNode root) {
        // If the tree is empty, we can say it’s balanced...
        if (root == null)  return true;
        // Height Function will return -1, when it’s an unbalanced tree...
		if (Height(root) == -1)  return false;
		return true;
	}
    // Create a function to return the “height” of a current subtree using recursion...
	public int Height(TreeNode root) {
        // Base case...
		if (root == null)  return 0;
        // Height of left subtree...
		int leftHeight = Height(root.left);
        // Height of height subtree...
		int rightHight = Height(root.right);
        // In case of left subtree or right subtree unbalanced, return -1...
		if (leftHeight == -1 || rightHight == -1)  return -1;
        // If their heights differ by more than ‘1’, return -1...
        if (Math.abs(leftHeight - rightHight) > 1)  return -1;
        // Otherwise, return the height of this subtree as max(leftHeight, rightHight) + 1...
		return Math.max(leftHeight, rightHight) + 1;
    }
}

111,Minimum Depth of Binary Tree

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: 2

Example 2:

Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5

Constraints:

The number of nodes in the tree is in the range [0, 105].
-1000 <= Node.val <= 1000

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {


    public int minDepth(TreeNode root) {
        if(root==null) return 0;

        if(root.left ==null && root.right==null){
            return 1;
        }else if (root.left == null){
            return minDepth(root.right)+1;
        }else if (root.right == null){
            return minDepth(root.left)+1;
        }
        int leftHeight = minDepth(root.left);
        int rightHeight = minDepth(root.right);
        return Math.min(leftHeight,rightHeight)+1;
    }
}

112,Path Sum

Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.

A leaf is a node with no children.

Example 1:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
Explanation: The root-to-leaf path with the target sum is shown.

Example 2:

Input: root = [1,2,3], targetSum = 5
Output: false
Explanation: There two root-to-leaf paths in the tree:
(1 --> 2): The sum is 3.
(1 --> 3): The sum is 4.
There is no root-to-leaf path with sum = 5.

Example 3:

Input: root = [], targetSum = 0
Output: false
Explanation: Since the tree is empty, there are no root-to-leaf paths.

Constraints:

The number of nodes in the tree is in the range [0, 5000].
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return false;
        }
        if (root.val == targetSum && root.left == null && root.right == null) {
            return true;
        }
        return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
    }
}

144.Binary Tree Preorder Traversal

Given the root of a binary tree, return the preorder traversal of its nodes’ values.

Example 1:

Input: root = [1,null,2,3]
Output: [1,2,3]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [1]
Output: [1]

Constraints:

The number of nodes in the tree is in the range [0, 100].
-100 <= Node.val <= 100

class Solution {
    private List<Integer> answer = new ArrayList<>();

    private void dfs(TreeNode node) {
        if (node == null) {
            return;
        }
        // Visit the root first, then the left subtree, then the right subtree.
        answer.add(node.val);
        dfs(node.left);
        dfs(node.right);
    }
    
    public List<Integer> preorderTraversal(TreeNode root) {
        dfs(root);
        return answer;
    }
}

we can use stack here.

public List<Integer> preorderTraversal(TreeNode root) {
    List<Integer> result = new ArrayList<>();
    Deque<TreeNode> stack = new ArrayDeque<>();
    TreeNode p = root;
    while(!stack.isEmpty() || p != null) {
        if(p != null) {
            stack.push(p);
            result.add(p.val);  // Add before going to children
            p = p.left;
        } else {
            TreeNode node = stack.pop();
            p = node.right;   
        }
    }
    return result;
}

145,Binary Tree Postorder Traversal

Given the root of a binary tree, return the postorder traversal of its nodes’ values.

Example 1:

Input: root = [1,null,2,3]
Output: [3,2,1]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [1]
Output: [1]

Constraints:

The number of the nodes in the tree is in the range [0, 100].
-100 <= Node.val <= 100

class Solution {
    public static void tree(TreeNode root,List<Integer>l){
        if(root==null) return;
        tree(root.left,l);
        tree(root.right,l);
        l.add(root.val);
    }
    
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer>l=new ArrayList<>();
        tree(root,l);
        return l;
    }
}

we can use stack here

public List<Integer> postorderTraversal(TreeNode root) {
    LinkedList<Integer> result = new LinkedList<>();
    Deque<TreeNode> stack = new ArrayDeque<>();
    TreeNode p = root;
    while(!stack.isEmpty() || p != null) {
        if(p != null) {
            stack.push(p);
            result.addFirst(p.val);  // Reverse the process of preorder
            p = p.right;             // Reverse the process of preorder
        } else {
            TreeNode node = stack.pop();
            p = node.left;           // Reverse the process of preorder
        }
    }
    return result;
}

this is for inorder traversal

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> result = new ArrayList<>();
    Deque<TreeNode> stack = new ArrayDeque<>();
    TreeNode p = root;
    while(!stack.isEmpty() || p != null) {
        if(p != null) {
            stack.push(p);
            p = p.left;
        } else {
            TreeNode node = stack.pop();
            result.add(node.val);  // Add after all left children
            p = node.right;   
        }
    }
    return result;
}

226,Invert Binary Tree

Given the root of a binary tree, invert the tree, and return its root.

Example 1:

Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

Example 2:

Input: root = [2,1,3]
Output: [2,3,1]

Example 3:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 100].
-100 <= Node.val <= 100

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        TreeNode right = invertTree(root.right);
        TreeNode left = invertTree(root.left);
        root.left = right;
        root.right = left;
        return root;
    }
}

257,Binary Tree Paths

Given the root of a binary tree, return all root-to-leaf paths in any order.

A leaf is a node with no children.

Example 1:

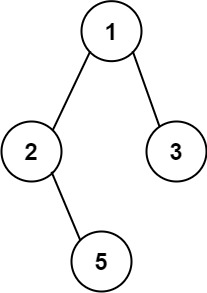
Input: root = [1,2,3,null,5]
Output: ["1->2->5","1->3"]

Example 2:

Input: root = [1]
Output: ["1"]

Constraints:

The number of nodes in the tree is in the range [1, 100].
-100 <= Node.val <= 100

public List<String> binaryTreePaths(TreeNode root) {
    List<String> answer = new ArrayList<String>();
    if (root != null) searchBT(root, "", answer);
    return answer;
}
private void searchBT(TreeNode root, String path, List<String> answer) {
    if (root.left == null && root.right == null) answer.add(path + root.val);
    if (root.left != null) searchBT(root.left, path + root.val + "->", answer);
    if (root.right != null) searchBT(root.right, path + root.val + "->", answer);
}

404, Sum of Left Leaves

Given the root of a binary tree, return the sum of all left leaves.

A leaf is a node with no children. A left leaf is a leaf that is the left child of another node.

Example 1:

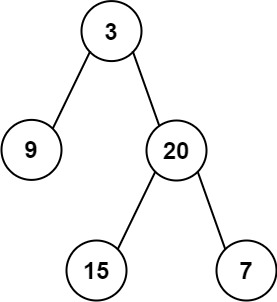
Input: root = [3,9,20,null,null,15,7]
Output: 24
Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.

Example 2:

Input: root = [1]
Output: 0

Constraints:

The number of nodes in the tree is in the range [1, 1000].
-1000 <= Node.val <= 1000

DFS

/**
 * DFS Recursive
 *
 * Time Complexity: O(N). All nodes will be visited.
 *
 * Space Complexity: O(H). Stack space.
 * In case of balanced tree (best case) it will be O(log N) and in case of Skewed Tree (worst case) it will be O(N)
 *
 * N = Number of nodes. H = Height of the tree.
 */
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }
		
		// Checking if left Node is a leaf node
        if (root.left != null && root.left.left == null && root.left.right == null) {
            return root.left.val + sumOfLeftLeaves(root.right);
        }

		// Exploring the tree further.
        return sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
    }
}

DFS Iterative (Pre-Order Traversal)

/**
 * DFS Iterative (Pre-Order Traversal)
 *
 * Time Complexity: O(N). All nodes will be visited.
 *
 * Space Complexity: O(H). Stack space.
 * In case of balanced tree (best case) it will be O(log N) and in case of Skewed Tree (worst case) it will be O(N)
 *
 * N = Number of nodes. H = Height of the tree.
 */
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }
		
		// In this solution we will also save if the node is a left node or not.
        Deque<Pair<TreeNode, Boolean>> stack = new ArrayDeque<>();
        stack.push(new Pair<>(root, false));

        int result = 0;

        while (!stack.isEmpty()) {
            Pair<TreeNode, Boolean> cur = stack.pop();
            TreeNode node = cur.getKey();
            boolean isLeft = cur.getValue();

            if (isLeft && node.left == null && node.right == null) {
                result += node.val;
                continue;
            }

            if (node.right != null) {
                stack.push(new Pair<>(node.right, false));
            }
            if (node.left != null) {
                stack.push(new Pair<>(node.left, true));
            }
        }

        return result;
    }
}

BFS Iterative This solution can take more space as the width of a complete tree will be TotalNumberOfNodes / 2. Thus, the queue space can increase upto O(N/2) in worst case.

/**
 * BFS Iterative
 *
 * Time Complexity: O(N). All nodes will be visited.
 *
 * Space Complexity: O(Width of the tree)
 * In case of a complete tree the width can be N/2. Thus worst case complexity = O(N)
 *
 * N = Number of nodes.
 */
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }

		// In this solution we will also save if the node is a left node or not.
        Queue<Pair<TreeNode, Boolean>> queue = new LinkedList<>();
        queue.offer(new Pair<>(root, false));

        int result = 0;

        while (!queue.isEmpty()) {
            Pair<TreeNode, Boolean> cur = queue.poll();
            TreeNode node = cur.getKey();
            boolean isLeft = cur.getValue();

            if (isLeft && node.left == null && node.right == null) {
                result += node.val;
                continue;
            }

            if (node.left != null) {
                queue.offer(new Pair<>(node.left, true));
            }
            if (node.right != null) {
                queue.offer(new Pair<>(node.right, false));
            }
        }

        return result;
    }
}